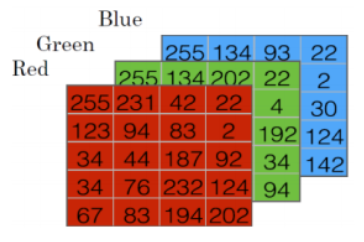
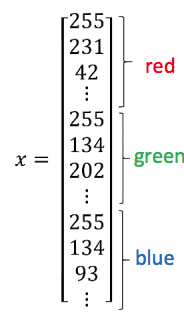
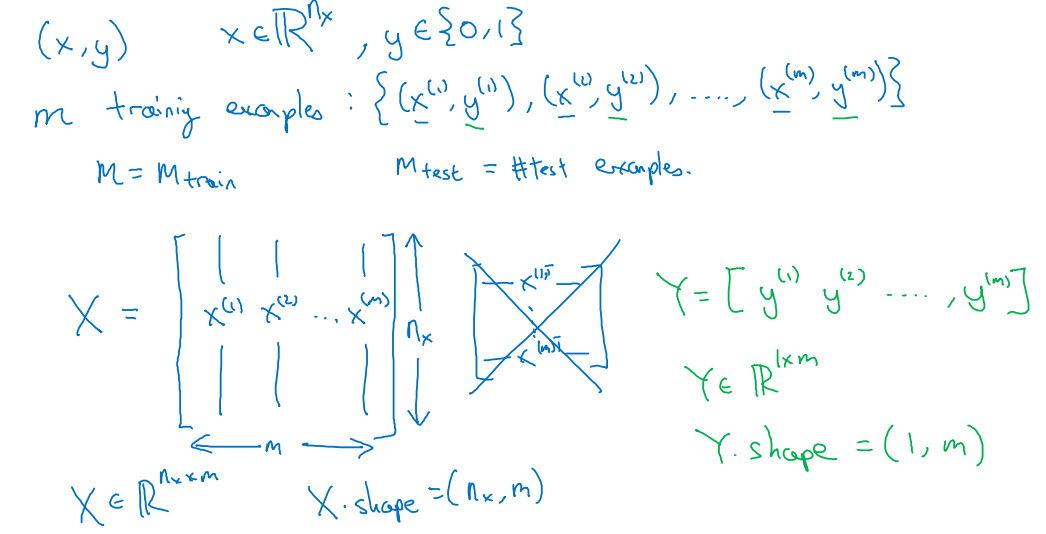
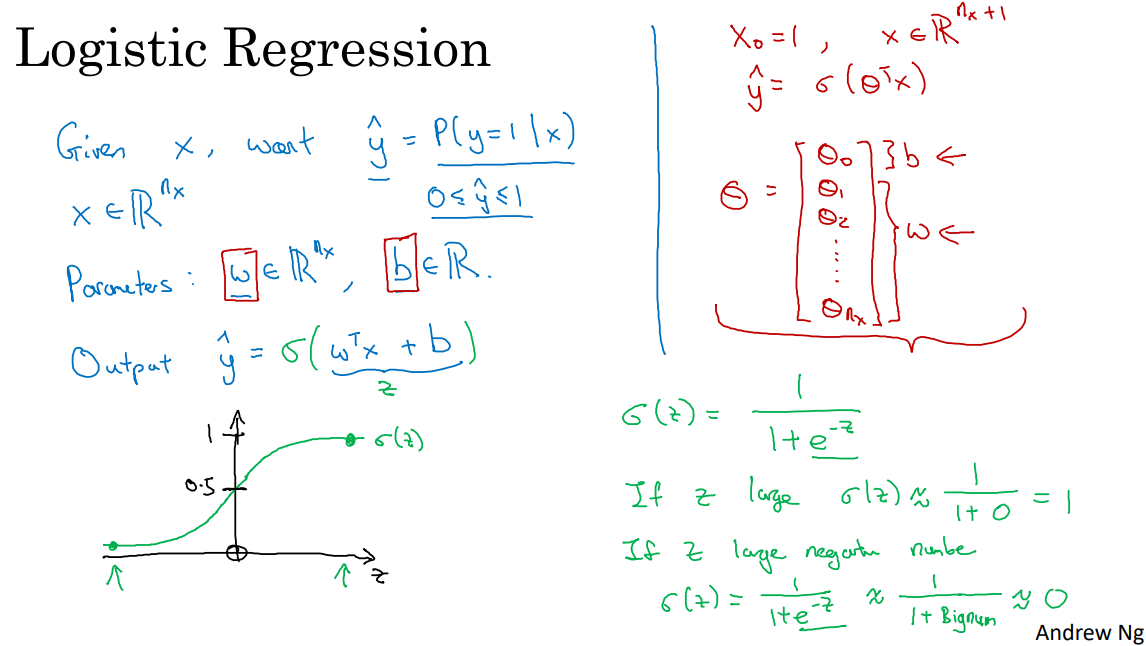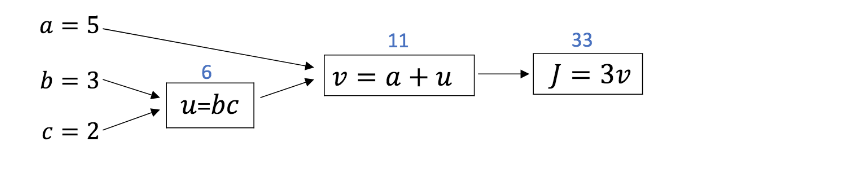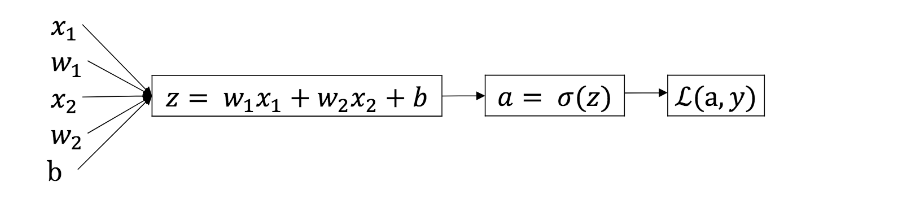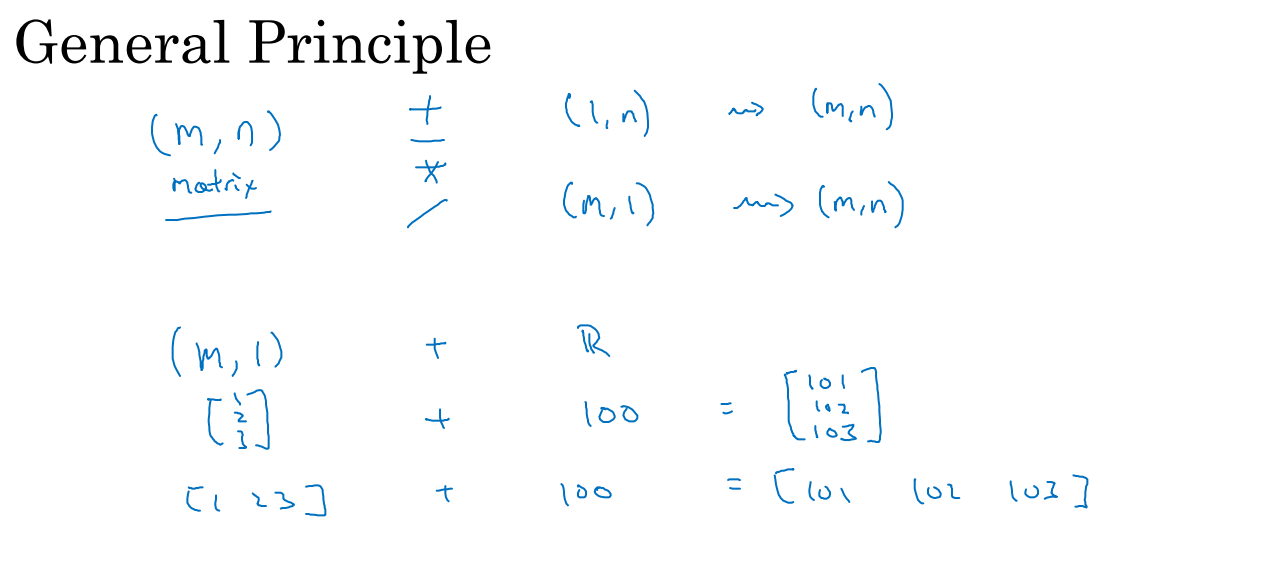표기법(Notation)¶
로지스틱 회귀(Logistic Regression)¶
로지스틱 회귀: 비용함수(Cost function)¶
$\hat{y}^{(i)} = \sigma(w^T x^{(i)} + b) \quad $ 여기에서 $ \sigma(z^{(i)}) = { 1 \over 1 + e^{-z^{(i)}} }$, $z^{(i)}=w^T x^{(i)} + b$, $ x^{(i)}$: i-th 훈련자료
$\{(x^{(1)}, y^{(1)}), \cdots, (x^{(m)}, y^{(m)})\}$ 에 대하여, 우리는 $\hat{y}^{(i)} \approx y^{(i)}$ 이 되길 원한다.
손실(Loss) 함수 (오류함수): $ \quad \mathscr{L}(\hat{y}^{(i)}, y^{(i)}) = { 1 \over 2} (\hat{y}^{(i)}-y^{(i)})^2 $
$$ \mathscr{L} (\hat{y}^{(i)}, y^{(i)}) = - \left[ y^{(i)} \log (\hat{y}^{(i)}) + (1-y^{(i)}) \log (1-\hat{y}^{(i)}) \right] $$$ y^{(i)} = 1 $ 이면, $\mathscr{L} (\hat{y}^{(i)}, y^{(i)}) = - \log (\hat{y}^{(i)})$ 가 되어, $\hat{y}^{(i)}$ 가 커야(즉, 1에 가까워야), 손실 $-\log (\hat{y}^{(i)})$ 가 작아지게 되며,
$ y^{(i)} = 0 $ 이면, $\mathscr{L} (\hat{y}^{(i)}, y^{(i)}) = - \log (1-\hat{y}^{(i)})$ 가 되어, $\hat{y}^{(i)}$ 가 작아야(즉, 0에 가까워야), 손실 $-\log (1-\hat{y}^{(i)})$ 가 작아지게 된다.
비용(cost) 함수: 비용 함수는 전체 훈련 세트의 손실 함수의 평균입니다.
$$ J(w, b) = { 1 \over m} \sum_{i=1}^m \mathscr{L} (\hat{y}^{(i)}, y^{(i)}) = -{ 1 \over m} \sum_{i=1}^m \left[ y^{(i)} \log (\hat{y}^{(i)}) + (1-y^{(i)}) \log (1-\hat{y}^{(i)}) \right] $$import numpy as np
import matplotlib.pyplot as plt
y_h = np.arange(0.01, 1, 0.05)
plt.subplot(121)
plt.plot(y_h, -np.log(y_h))
plt.xlabel('y_h')
plt.ylabel('- log(y_h)')
plt.grid(True)
plt.subplot(122)
plt.plot(y_h, -np.log(1-y_h))
plt.xlabel('y_h')
plt.ylabel('- log(1-y_h)')
plt.grid(True)
plt.show()
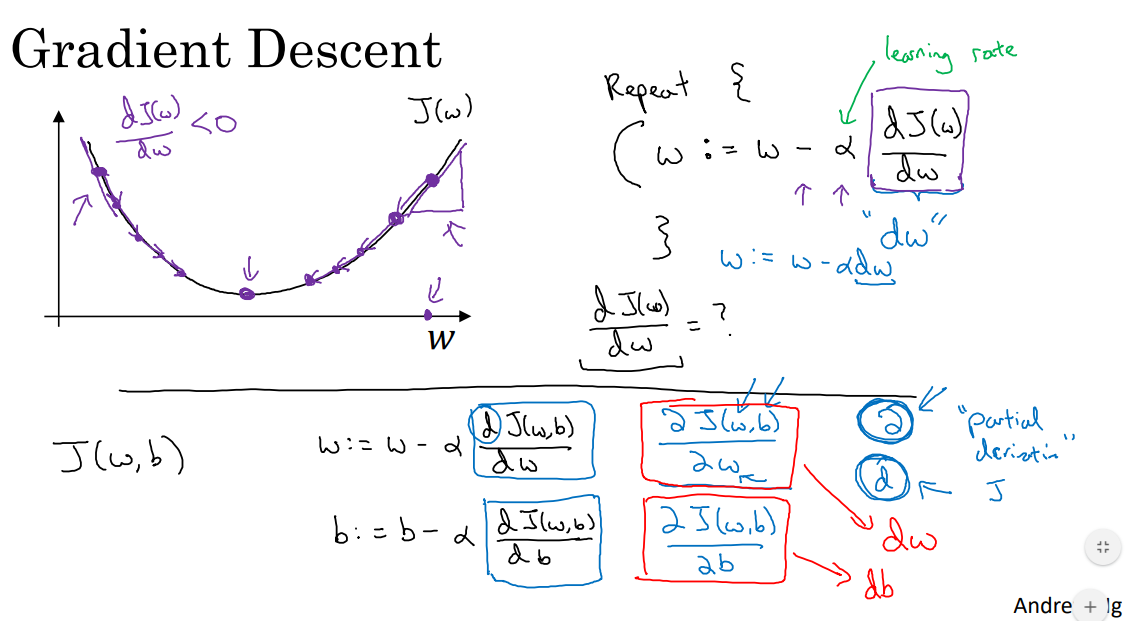
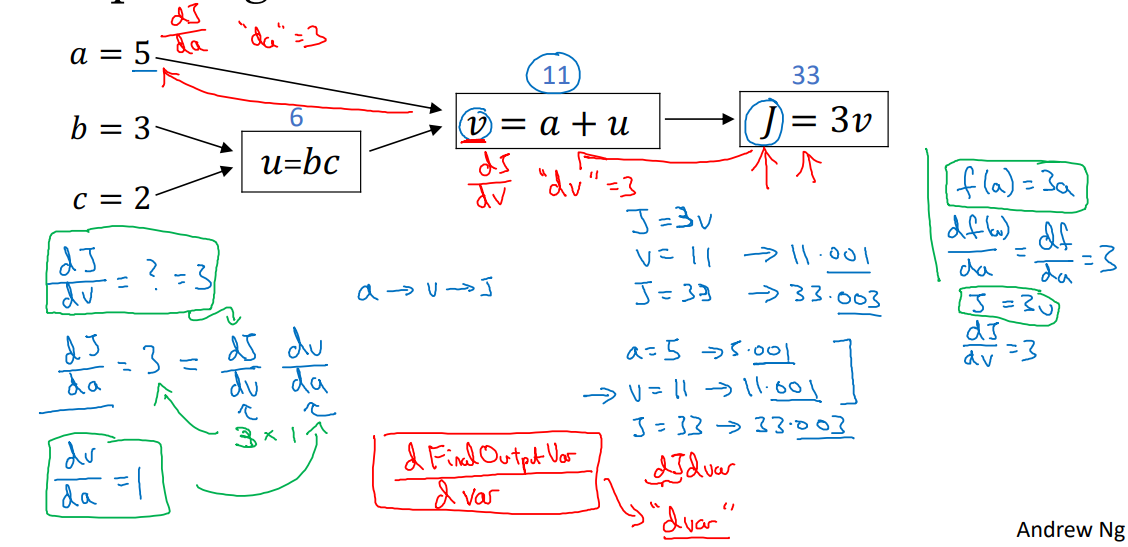
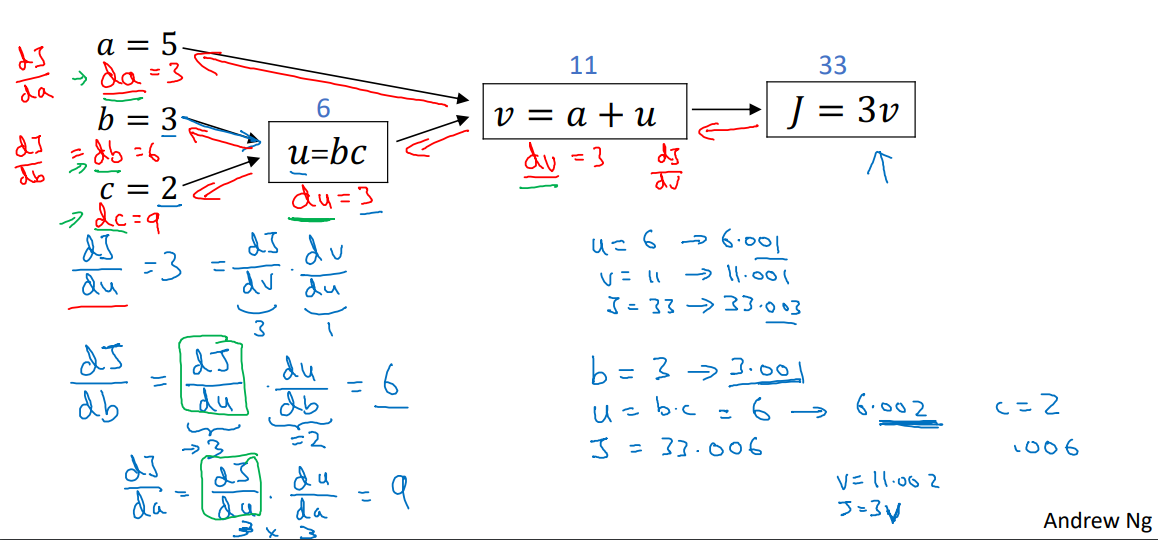
경사하강(Gradient descent)¶
단일 훈련자료에 대한 로지스틱 회귀 예측 모델은 다음과 같이 정의 되고
$\hat{y}^{(i)} = \sigma(w^T x^{(i)} + b) \quad $ 여기에서 $\quad \sigma(z^{(i)}) = { 1 \over 1 + e^{-z^{(i)}} }$
전체 훈련 세트의 손실함수의 평균인 비용함수는 다음과 같다. $$ J(w, b) = { 1 \over m} \sum_{i=1}^m \mathscr{L} (\hat{y}^{(i)}, y^{(i)}) = -{ 1 \over m} \sum_{i=1}^m \left[ y^{(i)} \log (\hat{y}^{(i)}) + (1-y^{(i)}) \log (1-\hat{y}^{(i)}) \right] $$
여기에서, $ J(w, b)$ 를 최소화하는 매개 변수 $w$ 와 $b$ 을 찾을 것입니다.
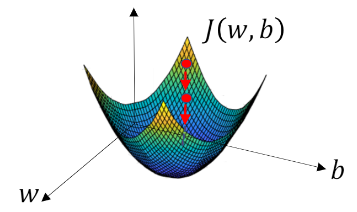
경사하강 (Gradient descent)¶
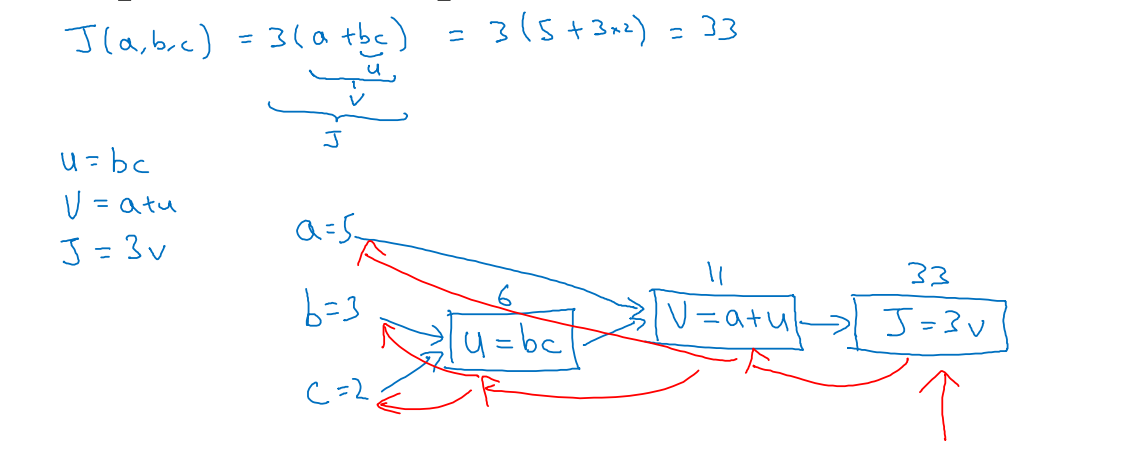
m개의 훈련 자료에 대한 경사하강¶
$$ J(w, b) = { 1 \over m} \sum_{i=1}^m \mathscr{L} (a^{(i)}, y^{(i)}) $$여기에서 $$ a^{(i)} = \hat{y}^{(i)} = \sigma(w^T x^{(i)}+ b) $$
$$ {\partial \over \partial w_1} J(w, b) = { 1 \over m} \sum_{i=1}^m {\partial \over \partial w_1} \mathscr{L} (a^{(i)}, y^{(i)})$$다음과 같이 약식으로, $$ {\partial \over \partial w_1} \mathscr{L} (a^{(i)}, y^{(i)}) \Rightarrow dw_1^{(i)} \text{ of } ( x^{(i)}, y^{(i)}) $$
m개의 훈련 자료에 대한 경사하강 : 구현¶
J = dw1 = dw2 = db = 0;
for i=1 to m:
z(i) = w_T*x(i) + b
a(i) = sigmoid(z)
J += - (y(i)*log(a(i)) + (1-y(i))*log(1-a(i)))
dz(i) = a(i) - y(i)
dw1 += x1(i)*dz(i)
dw2 += x2(i)*dz(i)
db += dz(i)
J /= m
dw1 /= m; dw2 /= m; db /=m;
import numpy as np
a = np.array([1,2,3,4])
a.shape
import time
a = np.random.rand(1000000)
b = np.random.rand(1000000)
print(a.shape, b.shape)
tic = time.time()
c = np.dot(a,b)
toc = time.time()
print("c = ", c)
print("Vectorization : ", str(1000*(toc-tic)), 'ms')
c = 0
tic = time.time()
for i in range(1000000):
c += a[i]*b[i]
toc = time.time()
print("c = ", c)
print("For loop : ", str(1000*(toc-tic)), 'ms')
벡터화(Vectorization) : 신경망 프로그래밍 지침¶
가능하면 명시적인 for 루프를 피하십시오.

벡터 및 행렬의 함수¶
행렬/벡터의 모든 요소에 지수 연산을 적용해야 한다고 가정해 보겠습니다.
$ v = \begin{bmatrix} v_1 \\ v_2 \\ \vdots \\ v_n \end{bmatrix} \quad \Rightarrow \quad u = \begin{bmatrix} e^{v_1} \\ e^{v_2} \\ \vdots \\ e^{v_n} \end{bmatrix}$
# For loop version ============
u = np.zeros((n,1))
for i in range(n):
u[i] = math.exp(v[i])로지스틱 회귀 미분 : 구현¶
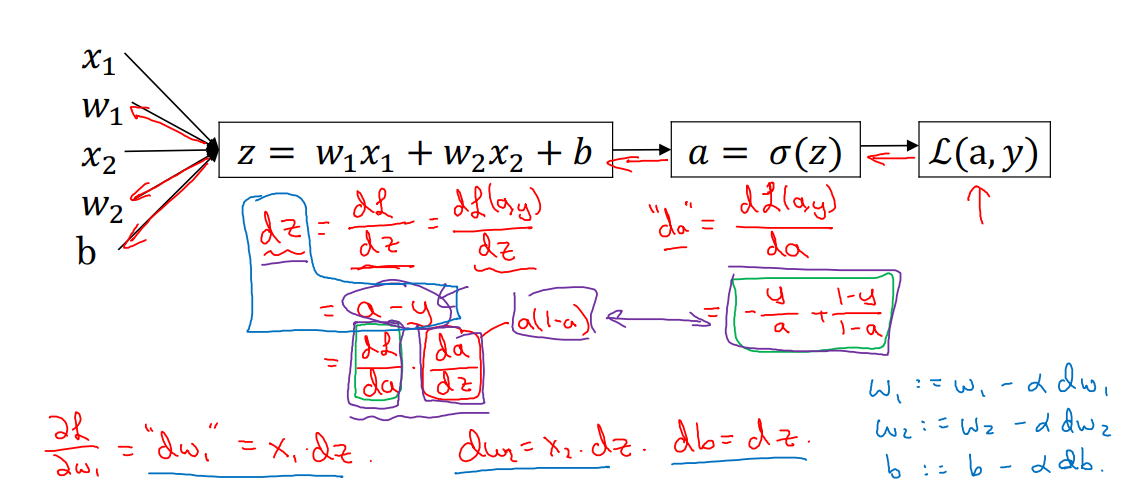
J = dw_1 = dw_2 = db = 0;
for i=1 to m:$\quad \quad \quad z^{(i)} = w^T x^{(i)} + b$
$\quad \quad \quad a^{(i)} = \sigma(z^{(i)})$
$\quad \quad \quad J += - [y^{(i)} \log \hat{y}^{(i)} + (1-y^{(i)}) \log (1-\hat{y}^{(i)})]$
$\quad \quad \quad dz^{(i)} = a^{(i)}(1-a^{(i)})$
$\quad \quad \quad dw_1 += x_1^{(i)}dz^{(i)}$
$\quad \quad \quad dw_2 += x_2^{(i)}dz^{(i)}$
$\quad \quad \quad db += dz^{(i)}$
J = J/m, dw_1 = dw_1/m; dw_2 = dw_2/m
db = db/m;로지스틱 회귀 벡터화¶
$$ z^{(1)} = w^T x^{(1)} + b \quad \quad \quad z^{(2)} = w^T x^{(2)} + b \quad \quad \quad z^{(3)} = w^T x^{(3)} + b $$$$ a^{(1)} = \sigma(z^{(1)})\quad \quad \quad \quad \quad a^{(2)} = \sigma(z^{(2)})\quad \quad \quad \quad a^{(3)} = \sigma(z^{(3)})$$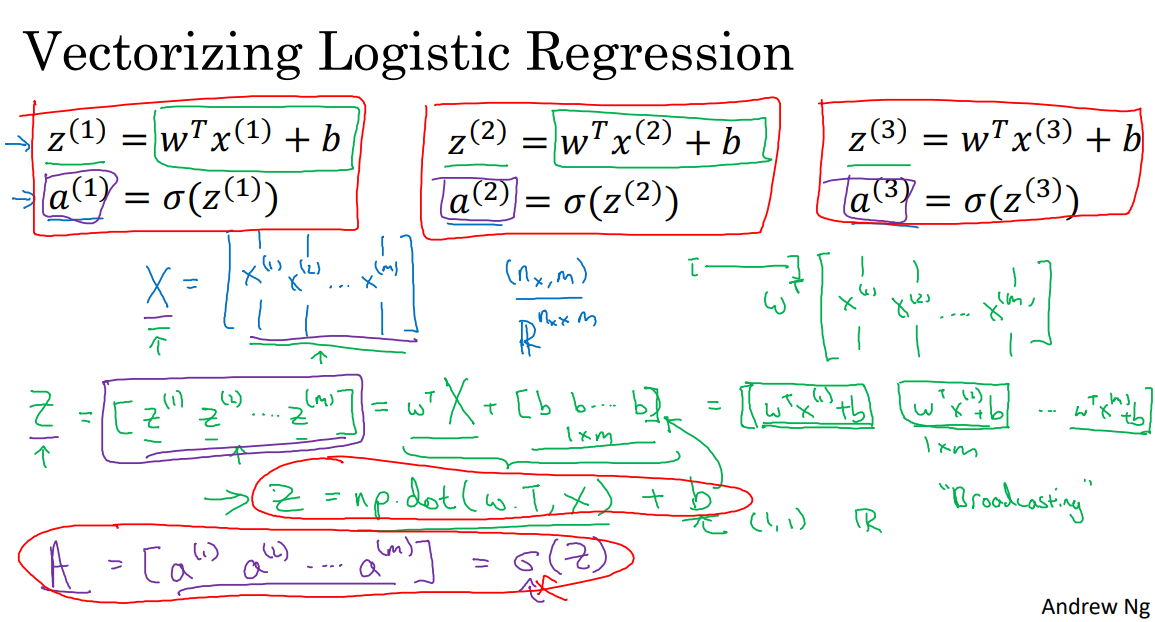
로지스틱 회귀 그래디언트 계산 벡터화¶

로지스틱 회귀 그래디언트 계산 벡터화 : 구현¶
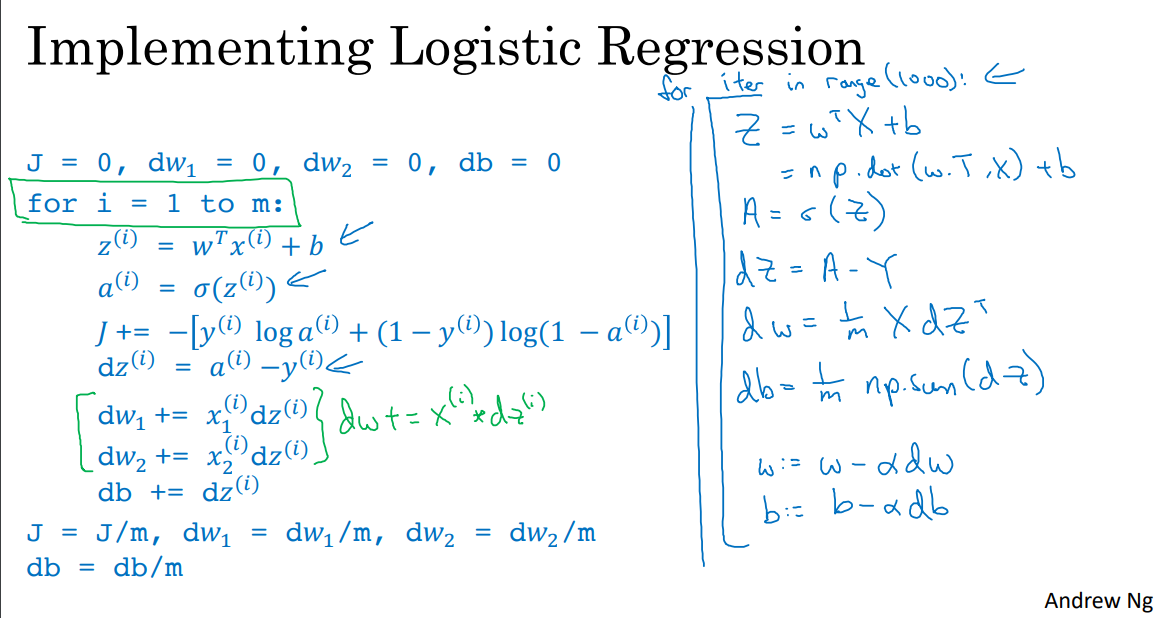
Broadcasting¶
(m,1) + (1,) ~> (m, 1)
$$ \begin{bmatrix} 1 \\ 2 \\ 3 \\ 4 \end{bmatrix} + 100 \quad \Rightarrow \quad \begin{bmatrix} 1 \\ 2 \\ 3 \\ 4 \end{bmatrix} + \begin{bmatrix} 100 \\ 100 \\ 100 \\ 100 \end{bmatrix}$$(m, n) + (1, n) ~> (m, n)
$$ \begin{bmatrix} 1, 2, 3 \\ 4, 5, 6 \end{bmatrix} + \begin{bmatrix} 100, 200, 300 \end{bmatrix} \quad \Rightarrow \quad \begin{bmatrix} 1, 2, 3 \\ 4, 5, 6 \end{bmatrix} + \begin{bmatrix} 100, 200, 300 \\ 100, 200, 300 \end{bmatrix}$$(m, n) + (m, 1) ~> (m, n)
$$ \begin{bmatrix} 1, 2, 3 \\ 4, 5, 6 \end{bmatrix} + \begin{bmatrix} 100 \\ 200 \end{bmatrix} \quad \Rightarrow \quad \begin{bmatrix} 1, 2, 3 \\ 4, 5, 6 \end{bmatrix} + \begin{bmatrix} 100, 100, 100 \\ 200, 200, 200 \end{bmatrix}$$import numpy as np
a = np.array([1,2,3,4])
# a = np.array([[1],[2],[3],[4]])
print(a, " + 100 = ", a+100)
b = np.array([[1,2,3],[4,5,6]])
c = np.array([100,200,300])
print(b.shape, " + ", c.shape, " = ", (b+c).shape)
print(b + c)
d = np.array([[100],[200]])
print(b.shape, " + ", d.shape, " = ", (b+d).shape)
print(b + d)
(Example) 100g의 다양한 음식에 포함된 탄수화물, 단백질, 지방의 칼로리가 다음과 같을 때,탄수화물, 단백질, 지방으로부터의 칼로리가 각각 몇 % 인지를 계산하는 문제가 있다.
| \ | Apples | Beef | Eggs | Potatoes |
|---|---|---|---|---|
| Carb | 56.0 | 0.0 | 4.4 | 68.0 |
| Protein | 1.2 | 104.0 | 52.0 | 8.0 |
| Fat | 1.8 | 135.0 | 99.0 | 0.9 |
위의 계산을 명시적인 for-loop 를 사용하지 않고 할 수 있는가?
import numpy as np
A = np.array([[56.0, 0.0, 4.4, 68.0],
[1.2, 104.0, 52.0, 8.0],
[1.8, 135.0, 99.0, 0.9]])
cal = A.sum(axis = 0)
print(cal)
percentage = 100 * A / cal
print(percentage)
print(A.shape, cal.shape, percentage.shape)
(선택 사항) 로지스틱 회귀 비용함수 설명¶
로지스틱 회귀 비용함수¶
로지스틱 회귀에서 주어진 $x$ 에 대한 추정 $\hat{y}$는 다음과 같이 계산됩니다. $$ \hat{y} = \sigma (w^T x + b) \quad\text{where}\quad \sigma(z) = { 1 \over 1 + e^{-z}}$$
그리고, 이는 $x$에 대하여 $y=1$일 확률, 즉, $ \hat{y} = P(y=1|x)$ 로 해석한다고 했습니다. 궁극적으로 우리의 알고리즘은 $ \hat{y}$ 이 입력 값 x에 대해서 $y$가 1일 확률을 나타내주길 바랍니다.
다시 말해, $y$가 1인 경우, 주어진 x에 대한 $y$ 일 확률이 $\hat{y}$이라고 할 수 있습니다. 반대로, 만약 $y$가 0 이면, $y$가 0일 확률은 $1- \hat{y}$이 됩니다. 따라서 $\hat{y}$ 은 $y$가 1일 확률이고, $1- \hat{y}$ 은 $y$가 0일 확률이 됩니다.
- $y=1$ 일 때는, $P(y|x) = \hat{y}$
- $y=0$ 일 때는, $P(y|x) = 1- \hat{y}$
로지스틱 회귀 비용함수¶
- $y=1$ 일 때는, $P(y|x) = \hat{y}$
- $y=0$ 일 때는, $P(y|x) = 1- \hat{y}$
위의 두 식을, 하나의 식으로 요약해보면 다음과 같이 됩니다.
$$ P(y|x) = \hat{y}^y (1-\hat{y})^{(1-y)}$$- $y=1$ 일 때는, $P(y|x) = \hat{y}^1 (1- \hat{y})^0 = \hat{y}$
- $y=0$ 일 때는, $P(y|x) = \hat{y}^0 (1- \hat{y})^{1} = 1- \hat{y}$
m 예제에 대한 비용¶
$$ P(\text{labels in training set}) = \log \prod_{i=1}^M P(y^{(i)} | x^{(i)})$$최우추정 (Maximum Likelihood Estimation) :
$$ P(\text{labels in training set}) = \sum_{i=1}^M P(y^{(i)} | x^{(i)}) = - \sum_{i=1}^M \mathscr{L}(y^{(i)},y^{(i)})$$Cost to minimize :
$$ J(w, b) = { 1 \over m} \sum_{i=1}^m \mathscr{L} (\hat{y}^{(i)}, y^{(i)}) $$